divisor game gfg potd Python solution 9 May 2024 | divisor game leetcode solution

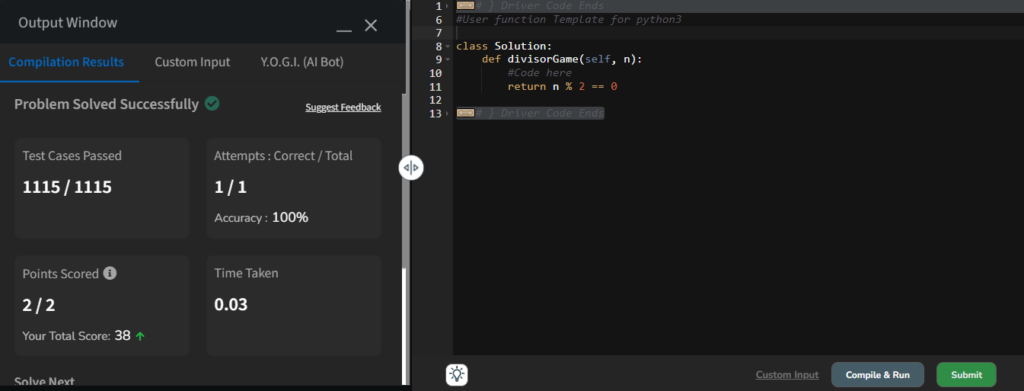
Today problem of the day on geeks for geeks potd is Divisor Game on gfg 9 May 2024. Divisor game problem has previously been asked on leetcode as well. This problem is an Easy level questions even more you will be amazed by looking at the solution, but the problem solving and thinking behind the divisor game problem is what matters. It can be easily asked by some of Service based MNC plc companies like IBM, Deloitte, Accenture or EY, PWC and KPMG and other highly anticipated tech giants and top IT firms.The reason being the strong and in depth analytical skill you require to find the right approach towards divisor game problem solution.

Please do not directly look for the solution for todays geeks for geeks problem of the day, instead go your own way, think about alternatives, that’s the only way to build the logic, try to learn the basic concepts about analytical and numerical questions based on odd-even nature of number and try to define an approach that you would take to solve divisor game problem using python or your favorite programming language. Have look into solution for Divisor game only if you are stuck.

To solve this problem, we can observe that the game has a winning strategy based on the value of n. If n is an even number, Alice can always win by subtracting 1 from n on her first move. This will leave Bob with an odd number, and since all the divisors of an odd number are odd, Bob will have no choice but to leave an even number for Alice. Alice can then continue subtracting 1 until she wins.

However, if n is an odd number, Alice cannot win no matter what move she makes. This is because any divisor x of n (except 1 and n) will result in an even number n - x, giving Bob the advantage to win the game.

Below is the Python code for the divisorGame function:

def divisorGame(n: int) -> bool:
    return n % 2 == 0

print(divisorGame(2)) # Output: True
print(divisorGame(3)) # Output: False

The time complexity of this solution is O(1) since it involves a constant-time operation (modulus operator), and the space complexity is also O(1) as we are not using any additional data structures.

Here’s a more detailed explanation of why this solution works:

1. If n is even, say n = 2k for some integer k, Alice can choose x = k on her first move. This will leave n - x = k on the chalkboard.
2. Now, no matter what move Bob makes, he will be left with an even number on the chalkboard, and Alice can continue subtracting 1 until the number becomes 0, winning the game.
3. If n is odd, say n = 2k + 1 for some integer k, any divisor x that Alice chooses will result in n - x = 2(k + 1) - x = 2m for some integer m, which is an even number.
4. This gives Bob the advantage, as he can now subtract 1 from the even number on the chalkboard, leaving an odd number for Alice.
5. Alice and Bob will continue alternating moves, but eventually, Alice will be left with an odd number on the chalkboard and no legal move to make, losing the game.

Therefore, if n is even, Alice has a winning strategy, and if n is odd, Bob has a winning strategy, assuming both players play optimally.

The time complexity of this solution is O(1) since it involves a constant-time operation (modulus operator), and the space complexity is also O(1) as we are not using any additional data structures.

Here’s a more detailed explanation of why this solution works:

1. If n is even, say n = 2k for some integer k, Alice can choose x = k on her first move. This will leave n - x = k on the chalkboard.
2. Now, no matter what move Bob makes, he will be left with an even number on the chalkboard, and Alice can continue subtracting 1 until the number becomes 0, winning the game.
3. If n is odd, say n = 2k + 1 for some integer k, any divisor x that Alice chooses will result in n - x = 2(k + 1) - x = 2m for some integer m, which is an even number.
4. This gives Bob the advantage, as he can now subtract 1 from the even number on the chalkboard, leaving an odd number for Alice.
5. Alice and Bob will continue alternating moves, but eventually, Alice will be left with an odd number on the chalkboard and no legal move to make, losing the game.

Therefore, if n is even, Alice has a winning strategy, and if n is odd, Bob has a winning strategy, assuming both players play optimally.